Autour d’une feuille de papier

Lors des Journées Nationales de l’APMEP, j’ai eu l’occasion d’assister à l’atelier de Sylvain ETIENNE intitulé « Autour d’une feuille de papier ». De nombreux points ont été abordés (dont certains bonus qui n’apparaissent pas dans le sommaire) :

• Plier en deux
• Format de papier
• Carré dans une feuille A4
• D’ailleurs, et Pythagore ?
• Octogone
• Plier en trois
• Pavé au milieu du cahier
• Agrandissement et réduction
• Nombre d’or
• Triangles
• Volume et pop corn
• Périmètre
• Papier toilette

Grâce aux documents mis à disposition par Sylvain, je vous propose un retour sur quelques moments forts de cet atelier.

Un format de papier très pratique

Une méthode simple pour retrouver le rapport entre la longueur et la largeur consiste à utiliser le rapport de réduction. En effet, si on souhaite que le ratio Longueur:largeur reste le même lorsque l’on plie la feuille en deux, cela signifie que le petit rectangle est une réduction du rectangle de départ. Or, son aire est divisée par 2. Cela implique donc forcément que ses longueurs sont divisées par \(\sqrt{2}\). En se concentrant sur les longueurs des deux rectangles, on obtient alors \(L=\sqrt{2}L_1\), soit \(L=\sqrt{2}l\).

Il est ainsi possible d’introduire une fonctions linéaire grâce aux différents formats de papier :

Plier une feuille A4 en 3

Quelle méthode pour plier parfaitement une feuille A4 en 3 afin de la faire rentrer dans une enveloppe ? Mise à part la méthode habituelle qui consiste à former l’accordéon du mieux possible… Il s’agit d’utiliser les ratios…

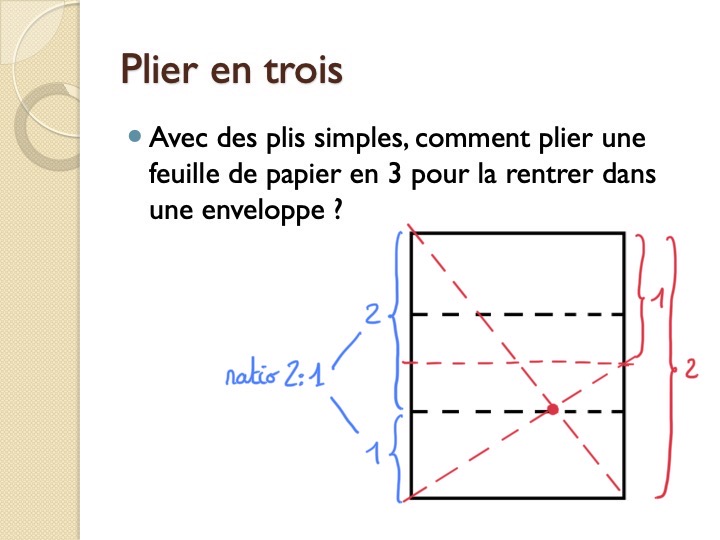
On voit apparaître un rapport de longueurs dans le ratio 2:1 dans le pliage en trois. Or, en pliant la feuille en 2, on obtient aussi deux longueurs dans ce même ratio (mais l’une est imbriquée dans l’autre). Il s’agit alors d’utiliser deux diagonales : l’une du rectangle de départ et l’autre de sa moitié. Le point d’intersection de ces deux diagonales indique où plier la feuille…

Un octogone dans une feuille A4

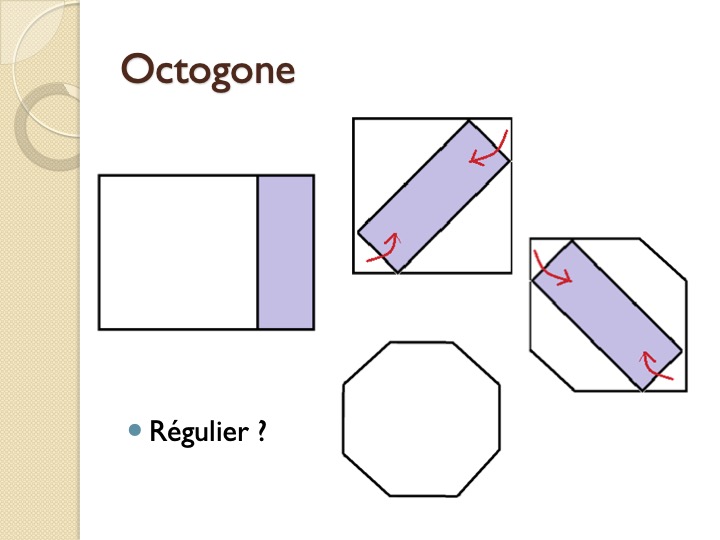
En suivant les indications de découpage, on obtient un octogone à partir du plus grand carré inscrit dans la feuille A4 comme par magie :

Une fois l’effet #Wahou passé (spécial dédicace à Manu H.), on se demande si cet octogone est régulier… Voici la vérification détaillée :

On a déjà vu que le rapport entre la longueur et la largeur d’une feuille A4 est de \(\sqrt{2}\).
Ainsi, on obtient que la largeur de la bande retirée dans la longueur pour former le carré est de \(\sqrt{2}a-a\).
Comme \(\sqrt{2}a-a\) est la longueur de la diagonale du carré de côté \(b\), on obtient alors que \(b=\displaystyle\frac{\sqrt{2}a-a}{\sqrt{2}}=a-\frac{\sqrt{2}}{2}a\).
Reste à calculer la longueur du côté \(c\), pour voir si l’octogone est régulier :
\(c = a-2(a-\displaystyle\frac{\sqrt{2}}{2}a)=a-2a+\sqrt{2}a=\sqrt{2}a-a\).
Comme la longueur de tous les côtés est de \(\sqrt{2}a-a\) alors cet octogone est bien régulier.

Un tétraèdre régulier en origami

Il s’agissait ici d’obtenir un triangle équilatéral par pliage puis, par extension, un joli tétraèdre régulier. Cela m’a rappelé ma séance d’inspection pour la titularisation car c’est l’activité que j’avais mené en seconde… Comme j’ai perdu ma version du tutoriel video, en voici un autre déniché sur Youtube :

Vous trouverez aussi une fiche proposée par Sylvain sur son site.

Volume et pop-corn

Nous avons aussi évoqué cette activité proposée par Dan Meyer au sujet du calcul de volumes (à partir d’une feuille de papier) :

Cela m’a fait sourire car j’avais l’impression de voir un problème Dudu… J’imaginais très bien les amis Arnaud et Julien faire la même scène au petit déjeuner le matin…

The fold and cut theorem

Je ne connaissais pas ce théorème mais il est vraiment puissant et intriguant : « il est possible de couper d’un seul coup de ciseau rectiligne n’importe quel polygone une fois qu’il a été plié de la manière adéquate ! ». Ce théorème a été démontré par Erik Demaine, Martin Demaine et Anna Lubiw en 1999 et ces derniers ont même publié un algorithme qui permet d’obtenir la carte des plis d’un polygone choisi.

Lors de l’atelier, nous l’avons fait pour le triangle équilatéral et il faut avouer que ce n’est pas difficile grâce à ses trois axes de symétries :

Sur le site d’Erik Demaine, on trouve des cartes de plis de polygones beaucoup moins symétriques et donc beaucoup plus impressionnants :

Conclusion

L’atelier proposé par Sylvain ETIENNE était vraiment très interessant et je n’ai évoqué ici qu’une partie de ce que nous avons abordé… Je suis vraiment content d’y avoir participé !